This handout covers the basic vector and matrix operations that you will need for 12-271.
This handout is adapted from Chapter 9 of Pascal with Applications in Science and Engineering, Susan Finger and Ellen Finger, D. C. Heath, Lexington MA, 1986.
Every branch of engineering uses vectors and matrices. This section will discuss vector and matrix notation and illustrate some of the basic operations used with vectors and matrices.
A vector is a physical quantity that has magnitude and direction. You can visualize a vector as an arrow with a specified length pointing in a particular direction. Some examples of quantities you can represent using vectors are: the velocity of a particle specified by its speed and direction of motion, the force on a wheel specified by the magnitude and direction of the force, and the position of a planet in space specified by its distance and direction from the sun. The last vector is illustrated below:

The magnitude of a vector is the absolute value of its length. The direction is given by the angle, in degrees or radians, from the positive x axis to the vector. A vector in polar coordinates is specified by its magnitude and angle. Polar coordinates are illustrated below:
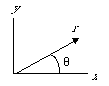
You can also represent a vector in cartesian coordinates. Cartesian coordinates are named for Ren Descartes (1596-1650) a French philosopher and mathematician and a contemporary of Pascal. In cartesian coordinates a vector is represented by its projection onto the x axis and its projection onto the y axis:
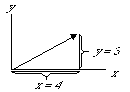
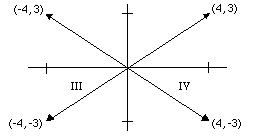
Not all vectors have positive coordinates. The figure below illustrates the following vectors in cartesian coordinates: [4,3], [-4,3], [-4,-3] and [4,-3]:
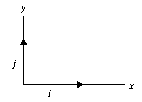
Because vectors are used so frequently in mathematics, science, and engineering, a compact standard notation for representing vectors has been developed. You must always specify the basis of a vector, that is the coordinate system in which the components are given. The most common basis is the cartesian coordinate system. The basis for this system in two dimensions is a vector with a length of one unit parallel to the x-axis and a vector with a length one unit parallel to the y-axis:
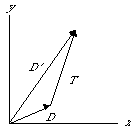
D = [ d1, d2 ]
where d1 is the component along the x-axis and d2 is the component along the y-axis. You can visualize the vector, D, as:
D[1] | D[2] |
|
|
The first cell of the array D stores the x coordinate of the
vector, and the second cell stores the y coordinate.
Similarly, you can visualize a vector represented in polar coordinates as:
D[1] | D[2] |
|
|
except the first cell now represents r, the magnitude of the vector,
and
the second cell represents
![]() ,
the angle that the vector makes with
the x-axis. This example emphasizes the importance of specifying
the basis
of a vector. The vector (1,1) in rectangular coordinates is
not the same
vector as (1,1) in polar coordinates.
,
the angle that the vector makes with
the x-axis. This example emphasizes the importance of specifying
the basis
of a vector. The vector (1,1) in rectangular coordinates is
not the same
vector as (1,1) in polar coordinates.
Because you can perform some vector operations more easily in polar
coordinates and others more easily in cartesian coordinates, you should know
how to convert between coordinate systems. You can find the polar coordinates,
r
and![]() , of a vector from its cartesian coordinates, x and y, by drawing
a simple diagram. Referring to the figure below, you can see that the vector
forms a right triangle with the x and y coordinates:
, of a vector from its cartesian coordinates, x and y, by drawing
a simple diagram. Referring to the figure below, you can see that the vector
forms a right triangle with the x and y coordinates:
You can use the Pythagorean theorem to write the formula for the hypotenuse, r:
r = (x2+ y2)½
You can find
![]() using
the relationship:
using
the relationship:
tan![]() = y/x
= y/x
or
![]() = tan-1(y/x)
= tan-1(y/x)
The function , tan-1, or arctan, returns the principal
angle
whose tangent is
![]() .
The principal angle is the angle in the first
or fourth quadrant whose tangent is
.
The principal angle is the angle in the first
or fourth quadrant whose tangent is
![]() .
The vectors [4,3] and [-4,-3]
will have the same arctan because y/x is equal to 4/3 in both cases. To
get the correct angle for vectors in the second or third quadrant, you must
add
.
The vectors [4,3] and [-4,-3]
will have the same arctan because y/x is equal to 4/3 in both cases. To
get the correct angle for vectors in the second or third quadrant, you must
add
![]() to the angle. This is equivalent to adding 180o to an angle expressed
in degrees.
to the angle. This is equivalent to adding 180o to an angle expressed
in degrees.
To convert from rectangular to polar coordinates, you must compute not only which quadrant a point is in, you must also consider what will happen if the point lies on the y axis. If the point lies on the y axis, then x is zero and the angle is "pi"/2 radians. What happens if x is equal to zero? To prevent division by zero, you must test the value of x before computing the angle. If x is zero, you must set the angle to "pi"/2.
To convert a vector in polar coordinates to cartesian coordinates, refer to the figure above again. Using the trigonometric identities, you can write x and y directly in terms of r and "theta":
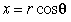
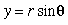
Vectors are not restricted to two dimensions. There are three-dimensional vectors, n-dimensional vectors, and infinite-dimensional vectors. While you cannot visualize vectors of more than three dimensions spatially, multi-dimensional vectors are used in many mathematical formulations of physical systems. In standard notation for multi-dimensional vectors, the components of an n-dimensional vector D, are represented by d1,d2,...dn:
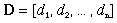
You can construct three-dimensional vectors that have three elements: one for the x-axis, one for the y-axis, and one for z-axis. In cartesian coordinates, three-dimensional vectors are given by their x, y, and z coordinates: [x,y,z].
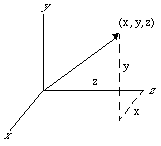
In scalar multiplication each element of the vector is multiplied by a constant. The result of scalar multiplication is another vector that has the same direction as the original vector, but whose magnitude has been changed by the value of the constant multiplier. The figure below shows a vector that scaled first by a factor of 2, and then by a factor of -2. The vectors are offset to show them more clearly:
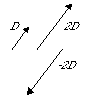
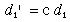
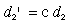
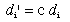 for i=1,2
for i=1,2
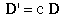
Graphically, you can add two vectors by drawing one vector and then drawing the second vector starting from the head of the first. Draw the resultant vector between the tail of the first vector and the head of the second vector:
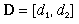
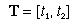
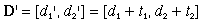
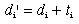 for i = 1,2
for i = 1,2
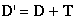
The dot and cross products are functions that operate on vectors in a multiplicative fashion. The definitions of these functions are, in some sense, arbitrary formulas for combining two vectors; however, both the dot product and the cross product are widely used in physics and engineering because they arise naturally in the solution of many problems involving vectors.
The dot product of two vectors, D and F, is defined to be the real number:
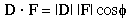
|D| is the magnitude of the vector D
|F| is the magnitude of the vector F
![]() is
the angle between the vectors D and F.
is
the angle between the vectors D and F.
The expression D"point"F is read as: D dot
F. The dot product is a scalar function of the two vectors, because
the magnitudes of the vectors are scalars as is
cos(![]() ).
So, the dot
product of two vectors is a single real number. For this reason, the dot
product is also referred to as the scalar product.
).
So, the dot
product of two vectors is a single real number. For this reason, the dot
product is also referred to as the scalar product.
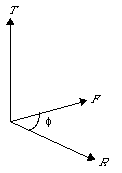
In physics, you use the dot product to compute the word. Work is defined as a force applied over a distance. To pull a massive block across a floor, you can attach a rope to the block and pull on the rope:
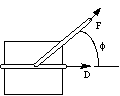
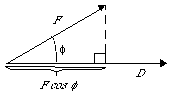
To compute the amount of force that contributes to the motion, you can take the projection of the force vector onto the distance vector. You can find the projection of vector F onto the vector by dropping a line, from the head of F perpendicular to D, creating a right triangle. One side of the new triangle lies along D. The new vector is the projection of F onto D. This vector represents the force that is useful in moving the block in the direction D. From the figure, you can see that the length of the projection is |F|cos("phi").
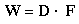
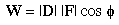
An alternate definition for the dot product of two vectors uses the rectangular coordinates, x and y, of the vectors. For example, you can represent the three-dimensional vector D by its components in the x, y, and z directions:
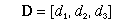
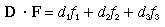
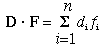
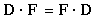
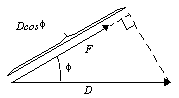
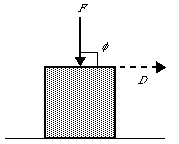
From the equation above, you can show that the dot product of two perpendicular vectors is zero. This result follows directly from the fact that the cos(90) is equal to zero. Applying this result to the problem of determining the work done by a force, suppose you push down (apply a downward force) on the block. No matter how hard you push, the block will not move forward. The downward force is perpendicular to the direction of motion, so no work is performed.
the first formula, D"dot"D is:
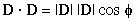
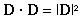
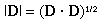
The cross product or vector product of two vectors, R and F, is a vector that is mutually perpendicular to the two vectors, with a magnitude of |R||F|sin("phi"), where "phi" is the angle between R and F.
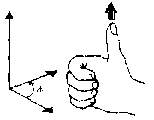
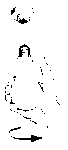
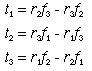
The cross product is not symmetric. Reversing the order of the vectors changes the sign of the resulting vector. The direction of the cross product, F x R, can be found by curling your fingers from F to R as illustrated below:
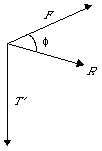
A common phenomenon that can be described using the cross product is torque. When you use a wrench to remove a bolt, you fix one end of the wrench to the bolt, and apply a force to the other end of the wrench. This force creates a torque:
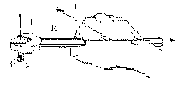
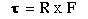
You can use a matrix to represent several vectors in a single mathematical structure. A matrix is a multi-dimensional array of numbers. For example, the two-dimensional matrix below is an array of 3 by 4 real numbers:
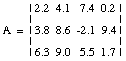
The elements of a matrix are specified by their row and column number: "a sub i,j". As with arrays, the row number is designated as i and the column number as j. For example, in the matrix above the element "a sub 3,2" has a value of 9.0. You can find this value by going down 3 rows and over 2 columns. The general form for an m by n matrix is:

In scalar multiplication of a matrix, each element is multiplied by a single constant value. If the matrix is R, and the scale factor is c, the elements in the new matrix R' are:
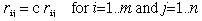
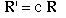
In matrix addition the corresponding elements of matrices are added together. Matrix addition is defined only for matrices that have the same dimensions. You cannot add a 2 by 2 matrix to a 10 by 10 matrix. If you add the elements of the matrix X to the matrix R, the the elements of the new matrix, R', are:
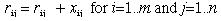
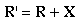
Matrix multiplication is a common operation. If you have never seen matrix multiplication before, it may take a while before it makes sense, but because you will use it so frequently in your work, it is worth the time to learn. In matrix notation, multiplication is written as:
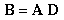
In matrix multiplication, you multiply the elements of one row of a matrix by the elements of one column of the other matrix. Sum the products and the result becomes the row,column element of the new matrix. If A is a m x n matrix and D is a n x l matrix, the elements of the new matrix are given by:
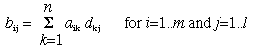

Under addition, matrices are associative and commutative. The additive inverse is -A, and 0 is a matrix with 0 for every element:
Associative: 
Commutative: 
Additive Inverse: 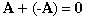
Under multiplication, matrices are associative, but they are not commutative.
Not Commutative: 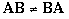
Multiplicative Inverse: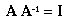
The multiplicative inverse is A"sup -1", and I is a square matrix with ones on the diagonal and zeros everywhere else.
sfinger@ri.cmu.edu